The concept of quantum computing has been around since the early 1980s when physicist Paul Benioff proposed a quantum mechanical model of the Turing machine. Benioff’s ideas were built upon by Richard Feynman, Yuri Manin, and others. He suggested that a quantum computer had the potential to simulate things that can’t be done using classical computing. In the 1990s, researchers began developing algorithms for quantum computing, such as Peter Shor’s quantum algorithm for factoring integers with the potential to decrypt RSA-encrypted communications, Lov K. Grover’s quantum search algorithm, and, more recently, quantum machine learning algorithms. These and other quantum computing algorithms will be discussed more in a later FAQ on “Applications and algorithms for quantum computing.”
Quantum computing continues to become increasingly sophisticated, with various relatively small-scale quantum computers being demonstrated today. However, most researchers believe that a commercially practical large-scale quantum computer is still relatively far in the future.
Just as quantum mechanics is a more general model of classical physics, quantum computing has the potential to be a disruptive, not an incremental, technology. The potential for quantum disruption of computing makes this technology compelling and provides motivation and commercial interest.
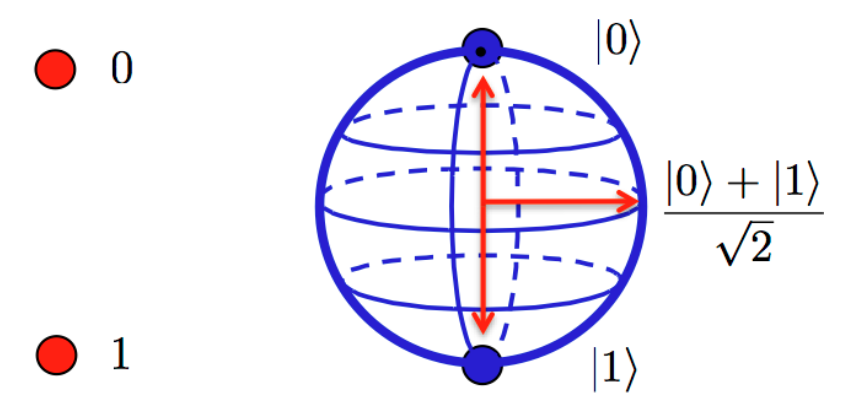
Quantum computing involves quantum phenomena such as quantum bits (qubits), superposition, entanglement, and decoherence (which is to be avoided). A “bit” in classical computing represents information as a series of discrete 0s and 1s. Bits are very different from qubits which can simultaneously exist in two states. A qubit is a two-level quantum system where the two basic qubit states are usually written as |0⟩ and |1⟩. |0⟩ is the Dirac notation for the quantum state that will always give the result 0 when converted to classical logic by a measurement, and |1⟩ is the state that will always convert to 1. A qubit can be in state |0⟩ or |1⟩ or (unlike a classical bit) in a linear combination of both states.
Physical systems such as an electron’s spin or the photon’s orientation are used to make qubits. These systems can simultaneously be in many different arrangements, a property known as quantum superposition. Qubits can also be inextricably linked together using a phenomenon called quantum entanglement. The result is that a series of qubits can represent different things simultaneously.
Eight classical bits can be used to represent any single number between 0 and 255. Eight qubits can simultaneously represent every number between 0 and 255. This is the source of the performance advantages of quantum computers compared with classical computers. Where there are many possible combinations, classical computers consider them one by one, while quantum computers can consider them all simultaneously. Unfortunately, qubits are extremely delicate and must be protected from all external interference to maintain their quantum properties of superposition and entanglement.
Superposition and entanglement
Quantum superposition and entanglement are fundamental concepts for quantum mechanics and computing. Superposition states that, like waves in classical physics, any two (or more) quantum states can be superposed or added together, and the result will be a valid quantum state. As a result, every quantum state can be represented as a sum of two or more other quantum states. Superposition is a property of the solutions to the Schrödinger equation. And, since the Schrödinger equation is linear, any linear combination of solutions will also be a solution.
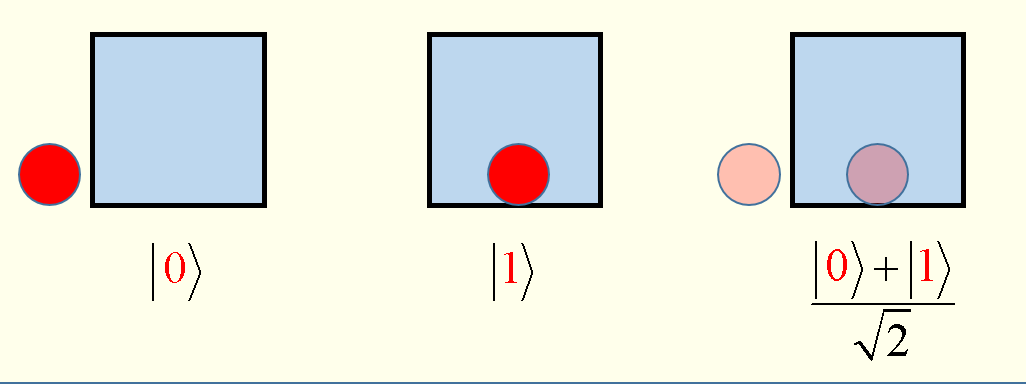
In quantum computing, the state of a qubit is a quantum superposition of |0⟩ and |1⟩. This means that the probability of measuring 0 or 1 for a qubit is not 0.0 or 1.0, and multiple measurements made on qubits in identical states will not always give the same result.
The inherent parallelism of quantum computers is a direct result of the superposition of qubits. It enables a quantum computer to perform multiple computations simultaneously, whereas a classical computer performs them one at a time. Theoretically, a 30-qubit quantum computer could equal the processing power of a conventional computer capable of running at ten teraflops. But it’s not that simple.
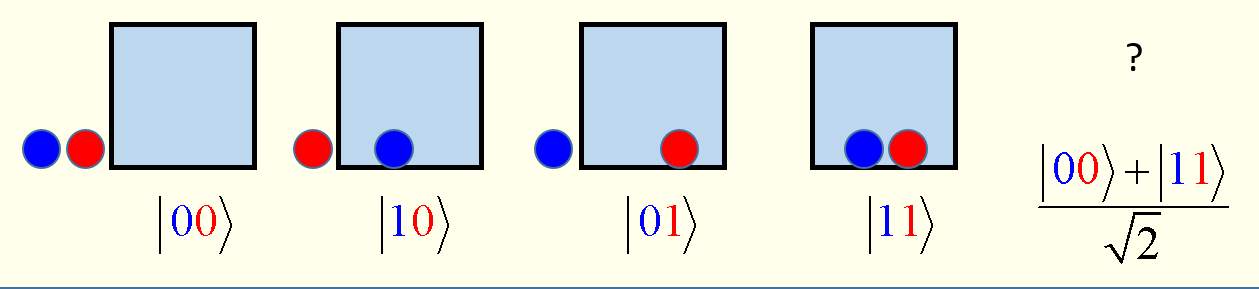
Quantum entanglement is another factor in quantum computing. Evaluation or measurement of the state of qubits is fraught with problems. Measuring a qubit in superposition to determine its value will cause it to assume a value of either 1 or 0, but not some combination of both. That effectively nullifies the operation of the quantum computer. Indirect measurements are needed to maintain the integrity of a quantum computer. Entanglement provides a possible answer.
In quantum physics, two qubits can become entangled, and the second qubit can take on properties related to the first qubit. If left alone, a qubit will assume multiple quantum states due to superposition. If a qubit is disturbed, it assumes one value; simultaneously, the second entangled atom will assume the opposite value. This allows engineers to know the value of the qubits without actually looking at them.
In addition, entanglement can be viewed as a computational power multiplier. As more and more qubits become entangled, the computing capabilities of the system grow exponentially. Unfortunately, entanglement is also a weakness. Even minute sources of interference will break the entanglement between two or more qubits. Qubits must only interact and entangle with each other. At the instant they have contact with outside forces, they stop working.
Roadblocks: interference and decoherence
Quantum interference is a byproduct of quantum superposition. Interference can be used to bias the measurement of a qubit toward a desired state or group of states. Under quantum interference, not only can an elementary particle be in more than one place at a time (superposition), but an individual particle, such as a photon of light, can cross its path and interfere with its trajectory.
Quantum interference can be easily disrupted. This disruption is called quantum decoherence and is a major source of errors when working with quantum computers. Any interaction of qubits with the outside environment in ways that disrupt their quantum behavior will result in decoherence.
Qubits are as fragile as they are powerful. The slightest vibration or change in temperature (called noise) will cause them to fall out of superposition and return to a classical physics state, causing the quantum computer to stop functioning.
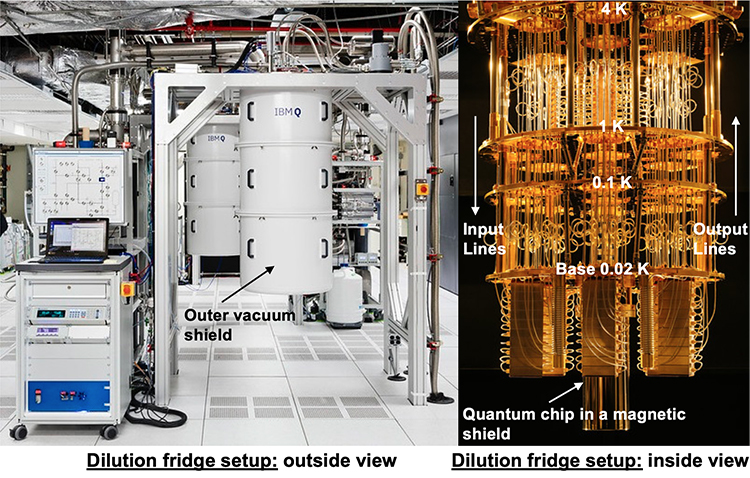
Vacuum chambers and supercooled environments are used to protect qubits from noise. Unfortunately, qubits are very sensitive, and noise still creeps in, causing many errors in quantum calculations. Improved quantum algorithms can help, and adding more qubits for error correction also helps. The bottom line is that it can take thousands of standard qubits to create a single highly-reliable unit called a “logical qubit.” That can offset much of the quantum computer’s computational capacity and advantage compared with classical computers.
The Hamiltonian
One of the concepts used in quantum computing is the Hamiltonian of a quantum system. The Schrödinger equation, which quantifies how the system’s wave function changes given the energy environment it experiences, governs the evolution of a quantum system. This energy environment is defined by the so-called Hamiltonian of the system, a mathematical description of the energies resulting from all forces felt by all system elements.
In addition to this difference in architecture (which will be the subject of the next FAQ on “Quantum computing system architectures and algorithms”), since quantum computers operate on different types of values than classical computers, they cannot use the same logical gate abstractions that were developed to manipulate classical bits. New abstractions for computations using qubits are required, providing a way to implement specified changes in quantum states. As with all quantum systems, the state of a qubit can be changed by changing its energy environment, which is the physical manifestation of its Hamiltonian.
How to quantum compute
Quantum computers complete calculations using the probability of a qubit’s state before it’s measured. In quantum computing, operations use the quantum state of qubits. These states are the undefined properties before they’ve been detected, such as an electron’s spin or a photon’s polarization. Instead of having a single definition, unmeasured quantum states occur in superposition. In a quantum computer, these superpositions are entangled with the states of other objects, meaning that their final outcomes are mathematically related, even if they are initially uncertain.
Being able to program a quantum computer is important. There are several tools available. One example is Qiskit, an open-source SDK for working with quantum computers at the level of pulses, circuits, and algorithms that uses Python. For seasoned developers interested in exploring potential quantum computing applications, the Qiskit element Aqua (algorithms for quantum computing applications) offers a library of algorithms for artificial intelligence, chemistry, finance, and optimization.
Summary
Even though the concept of quantum computing originated in the early 1980s, this is still a very nascent field. Quantum computing continues to become increasingly sophisticated, with a variety of relatively small-scale quantum computers being demonstrated today. However, quantum computers are fragile systems, and there are still substantial challenges to be overcome before the goal of “quantum supremacy” is achieved, enabling the demonstration of a programmable quantum computer that can solve a problem that no classical computer can solve in any feasible amount of time.
References
Quantum Computing – Progress and Prospects, The National Academies of Sciences, Engineering, Medicine
Qiskit, GitHub
Richard Feynman, On quantum physics and computer simulation, courtesy of Los Alamos National Laboratory
What are quantum technologies?, Sirteq