Various types of processors (DSPs, MCUs, etc.) have the ability to do math using floating point numbers, but what exactly does this mean? In general, floating point math offers a wider range of numbers and more precision than fixed point math. Knowing the difference, and when to use which type of math can make a difference in terms of a faster calculation or a more precise calculation. Mostly, the objective is to use only as much calculating power as you will need to get the job done.

A fundamental difference between the two is the location of the decimal point: fixed point numbers have a decimal in a fixed position and floating-point numbers have a sign. Both types of numbers are set up in sections, and there’s a placeholder for every portion of a number. Referring to Figure 1, fixed point numbers have a certain number of reserved digits that are on the left side of the decimal for the integer portion of the number. The numbers to the right of the decimal point are reserved for the fractional part of the number. If your MCU only uses fixed numbers, the decimal stays in the same place in that if two digits are set for the fractional portion, then that is the level of precision you will have going forward.

Very large numbers and very small numbers will have to fit in the same number of placeholders, what is actually bits, separated by the decimal in the same place, regardless of the number. For instance, if a fixed-point format will represent money, the level of precision might be just two places after the decimal. The programmer, knowing the register need hold only two bits after the decimal point, can put in 9999 and know that the fixed-point unit will interpret that number as 99.99, which is $99.99. (Here, base-10 numbers are used as an example, but recall that processors use base-2 or binary numbers).

Similarly, the number 001 would be interpreted by the code as 0.01. Decimals are left out of the code itself. Using the above money example again, the number 100 would be seen by fixed-point math as 1.00. The code for a fixed-point processor is written with respect to the decimal, which is in a fixed position. Fixed point math, independent of processor speed, is easier to code with and faster than floating point math. Fixed point is adequate unless you know that you will be dealing with higher numbers than the fixed-point unit can handle. Fixed-point numbers often are set up to use the most significant bit to represent a positive or negative sign. This means that a 4-bit unsigned integer has a range of 0 to 15 (because 2⁴ = 16), while a 4-bit signed integer has a range of -8 to 7 (-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7). Again, this is because, in a number that has only 4 bits in which to represent it, there are only 16 total possible numbers that can be represented. (I.e., 2⁴ = 16, where 4 is the total number of bits wide that the processor can handle in this example). Some recommend to never store money as a floating-point value.

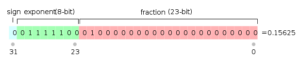
Floating point numbers also fit into a specific pattern. In fact, the Institute of Electrical and Electronics Engineers (IEEE) has a standard for representing floating-point numbers (IEEE 754). A floating-point number doesn’t have a fixed number of bits before and after a decimal. Rather, a floating-point number is defined by the total number of bits reserved for expressing a number. Like fixed-point numbers, floating point numbers have a pre-determined number of bits to hold the floating-point number, which has a sign (positive or negative number) as well as a number (i.e., mantissa) with an exponent. All of this has to fit in the data path allotted for the processor, which could be 16-bit, 32-bit, or 64-bit, etc. (See Figure 2 for how a 32-bit wide floating point number might be expressed.) Floating point numbers store as many precision bits as will fit in the data path, and the exponent determines the location of the decimal point in relation to the precision bits. The length of the exponent and mantissa would reflect the largest and smallest numbers anticipated by the application.

Floating-point numbers lose precision in that they only have a fixed number of bits with which to express a real number (e.g., 16-, 32- or 64-bit). Real numbers can go on to positive or negative infinity, and there is an infinite number of real numbers between 0 and 1, as well. A 16-bit processor has only 16-bits with which to represent numbers and is therefore capped at 2¹⁶. For example, a 4-bit processor has only 4 bits in which to represent numbers and is capped at 9999 as its highest number (if it doesn’t use one bit for a sign). A 16-bit processor can only represent 2¹⁶ different numbers.

Floating point numbers can seem confusing and complicated, but it’s also time-consuming for a processor. Doing math using floating point numbers can involve several steps to account for differences in exponential values. The IEEE 754 standard, first published as late as 1985, resolved problems having to do with creating portable code with respect to floating point conventions. Prior to the standard, companies handled floating point math as they saw fit, making code difficult to port from one type of processor architecture to another. The latest update to the standard was made in 2008. Several java-script based online tools are available for helping with understanding IEEE-754 floating point numbers using base-2. (Search for “IEEE-754 converter”.) Many articles and white papers have been written about how to best use floating point numbers since processors can be quite literal in comparing numbers and overflowing the highest possible number is going to roll the number over to zero. Simply put, floating point numbers can be much more complicated than fixed numbers with regard to how processors handle them.